概述
在安硕融资租赁云平台项目中有幸接触到融资租赁的核心功能–租金测算。目前的租金测算功能除调息功能外已经包含租赁行业的租赁业务场景,基本场景有:A.等额租金、B.等额本金、C.不等期确定本金 、D.等期不等额租金/不等期确定租金。 现就目前的测算功能进行分析,包括租金测算的模型设计、实现方式、核心算法、适用场景、各模块关联、以及一些概念的理解等。
专业术语解释
为了更好的理解租金测算模块,在开始了解其设计实现之前先介绍一下租金测算中用到的一些专业术语以及业务含义。
- 年利率:指一年的存款利率。所谓利率,是“利息率”的简称,就是指一定期限内利息 额与存款本金或贷款本金的比率;
-
XIRR:现金流的内部收益率,按年计算,现金流金额以及日期直接影响XIRR的值;
- 明示利率:签署合同时,需向承租方展示年利率;
-
隐含利率:签署合同时,不需向承租方展示年利率,只需约定每期还款金额;
- 按日计息:利息 = 上期未收本金* 年利率 * 实际天数/年计息天数;
-
按月计息:利息 = 上期未收本金* 年利率 * 间隔月数 * 30/年计息天数;
- 等期等额租金:租赁期间还款间隔相等,每期所还租金相同的还款计算方式;
- 等期等额本金:租赁期间还款间隔相等,每期所还本金相同的还款计算方式;
- 等期不等额租金:租赁期间每期还款间隔相等,每期所还租金不等的还款计算方式;
- 不等期确定本金:租赁期间还款间隔不一定相等,确定每期所还本金,计算每期所还租金;
- 不等期确定租金:租赁期间还款间隔不一定相等,确定每期所还租金,计算每期所还本金;
设计实现
设计思路
因为整个云平台是使用DDD模型来进行设计实现的,所以租金测算模块也是依靠该模型进行设计的。但是由于租金测算界面以及交互逻辑的复杂性,它和其他模块又有一些区别。最终的解决方案是将租金测算的各个小界面进行单独设计dsl,在API层面进行大的整合。后端接收请求进行计算,然后将数据传给前端进行渲染。最终渲染不走前端框架,而是由前端自定义界面来负责渲染,包括很大一部分的交互及逻辑都是固化在前端代码中的。
- 前端调用Render方法获取dsl,进行界面渲染;
- 初始化报价数据、资金计划,点击计算;
- 按照报价数据加载对应计算器,根据相应参数进行计算;
- 将计算结果包装并返回给前端进行渲染;
- 前端拆分数据,各个tab页分别进行展示;
实体模型设计
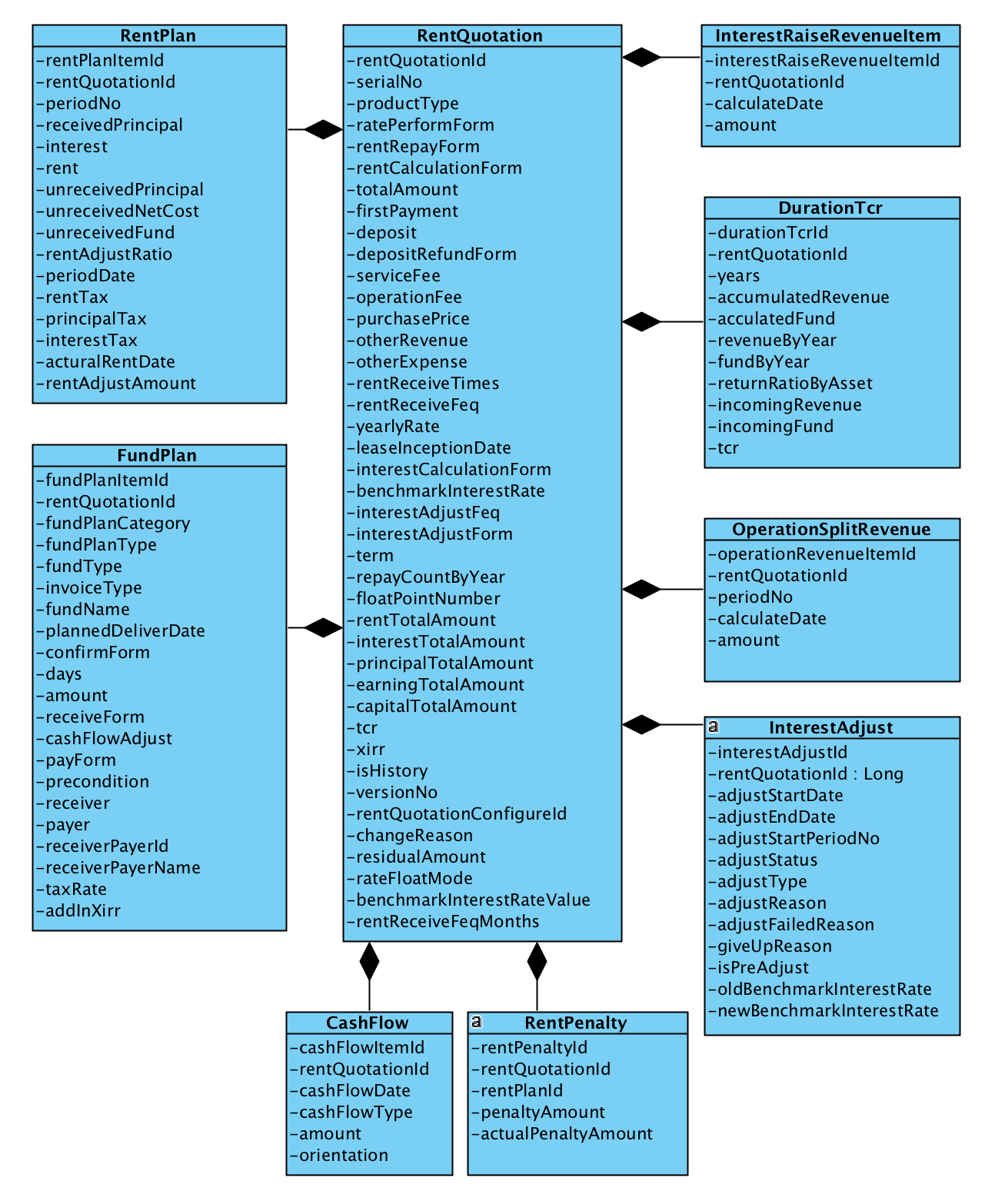
租金算法
后端实现主要还是要理解租金算法,这才是租金测算模块的核心,所以就没必要复制粘贴代码了。
目前系统中实现了五种算法,上面已经进行了基本含义介绍,其实在算法设计中主要计算方式只有两种,等期等额租金、等期等额本金。剩余三种算法都是在等额本金算法算出的基础数据上进行修改再进行计算的。
算法简介
-
等期不等额租金:该算法实际操作时,应先按照等期-等额租金的逻辑计算一版测算表,然后用户将”租金计算方式“改成”等期-不等额租金“,获得修改每期租金的权限,再进行修改测算出不等额租金的结果;
-
不等期确定租金:该算法实际操作时,应先按照等期-等额租金的逻辑计算一版测算表,然后用户将”租金计算方式“改成”不等期-确定租金“,获得修改日期和每期租金的权限,再进行修改测算出不等期确定租金的结果;
-
不等期确定本金:该算法实际操作时,应先按照等期-等额租金的逻辑计算一版测算表,然后用户将”租金计算方式“改成”不等期-确定本金“,获得修改日期和每期本金的权限,再进行修改测算出不等期确定本金的结果;
这三种算法都是在等期等额租金的算法基础上进行修改的,只是对一些收益进行重新计算不涉及大量的逻辑计算,在实际业务场景中应该也是较为少见。所以我们首先介绍等期等额租金和等期等额本金的算法逻辑。
注意要点
- 无论是哪种算法都要保证 每期租金 = 回收本金 + 利息;
- 明示利率间隔利率为已知数,可以根据年利率、起租日、每期间隔月数等字段计算出每期间隔利率;
- 无论是哪种算法都要在最后一期进行特殊处理,将最后一期差额在利息中轧平;
- 如果存在资产余值,最后一期的未回收本金 = 资产余值;
等期等额租金(矩阵法)
- 第一步 设:每期租金:A;每期利率:Rn(指还租间隔之间的期利率) ; 总本金:M(项目总额-首付款);每期所还本金:Xn; (其中:按日计息:Rn=年利率(n期的租金日-n-1期的租金日)/年计息天数,按月计息:Rn=年利率(n期的租金月-n-1期的租金月)*30/年计息天数;M=项目总额-首付款;)
-
第二步,根据“租金=利息+回收本金”列示每一期的方程式:

- 第三步,将已知数和未知数分别替换到等式的两边,如下图所示:

- 第四步,提炼矩阵,利用逆矩阵求出变量A、Xn

- 第五步,解出租金和每期本金,再带入公式利息(未还本金*期利率)=租金-本金,算出利息后将租金计划拼装完整。
等期等额租金(折现法)
设:每期终值(FV):A 每期利率:Rn(指还租间隔之间的期利率)
总本金:M(项目总额-首付款) 每期现值(PV):Xn(与每期所还本金无关)

利用二分法求解,未知数为A,范围在0~M之间, 最后在误差 < 1×10^-12
求出A的值以后,再带入公式租金-利息(未还本金*期利率)=本金,算出租金计划各值。
-
算法比较
等额租金的算法有很多,但是总的原理是相同的,都是依照:利息=未还本金 * 间隔利率,可参考附录中《PMT算法推导》。矩阵算法和PMT算法原理相同,因为PMT采用二分法,算出的值相对不是很准确,不过误差在小数点后10位以后,可以不考虑误差。算法时间上二分法稍快一点,60租期,时间比矩阵算法快几十毫秒,但是误差上折现法较大,不够精确,所以现在系统中使用矩阵算法。
等额本金
每期本金:X , 总本金:M(项目总额—收付款) , 期数:n 每期利率:Rn(指还租间隔之间的期利率) , 每期租金:An

该算法较为简单,只需保证 租金 = 本金 + 利息 即可精确算出租金计划,基本不会存在误差。
不等期确定本金
与等额本金很类似,只不过每期本金不相等,但是由于是确定本金,所以每期本金是已知数。 每期租金:An, 每期利率:Rn, 总本金:M, 每期所还本金:Xn

等期不等额租金/不等期确定租金(明示利率)
每期租金:An, 每期利率:Rn, 总本金:M, 每期所还本金:Xn

因为确定租金/明示利率,不论租金,本金还是利率都是已知的,所以只需按照公式用循环从第一期循环处理至最后一期就可以。
最后一期差额在利息中轧平(An-Xn)
等期不等额租金/不等期确定租金(隐含利率)
年利率为:R(0%—100%), 每期间隔天数:Dn , 总本金:M, 每期租金:An , 每期本金为:X , 年记天数:Y

根据M=X1+X2+…+Xn公式,将R从0到100%进行二分法切分
- R=50%
- R=25%
- R=12.5% …… 直至满足公式:M=X1+X2+…+Xn
各模块关联
测算报价(RentQuotation)

测算报价是租金测算中由客户录入的报价数据,该数据录入才是租金测算的起始点,报价数据包括租赁方式、价格信息、期限及利率、收益情况四个部分。前三个模块基本上是由用户录入而来,收益情况则是完全是计算出来的。该部分主要有几点需要注意:
- 租金偿还方式先付或者后付对租金还款日、还款金额以及资金占用等收益情况都会有影响;
- 产品总额 - 首付款 = 租金总额;
- 留购价款应该在租赁终止日期时算入现金流,因为现金流日期对XIRR会有较大影响;
- TCR仅受总收益和总资金占用影响;
租金计划(RentPlan)
租金计划是测算模块的一个重要的模块,也是测算是否精确的依据,只要租金表足够精确,其他模块的问题都可以单独解决。在测算算法中会对这一模块进行详细的介绍,主要有几点在计算时需要特别注意:
- 无论是哪种算法都要保证 每期租金 = 回收本金 + 利息;
- 无论是哪种算法都要在最后一期进行特殊处理,将最后一期差额在利息中轧平;
- 如果存在资产余值,最后一期的未回收本金 = 资产余值;
资金计划(FundPlan)
目前报价设计中的资金计划基本为报价详情中的价格信息的体现。在计算之前就要进行资金计划的初始化,根据需求将报价中的价格信息体现在资金计划中,主要用途是进行现金流的体现,XIRR的计算,以及后续核销使用。
- 资金计划初始化以后用户可以修改资金计划的时间,继而影响现金流的时间,这会对XIRR有较大影响;
- 资金计划中有一字段”是否计入XIRR”,该字段不影响现金流的显示,但是在计算时要将不计入XIRR的现金流过滤;
现金流(CashFlow)
现金流可以衡量真实的资金往来,更加准确的计算收益和计量成本。现金流的计算逻辑实为资金计划和租金计划的实际金额流传的汇总。之前业务中报价系统影响现金流的业务场景主要有两种,一种为“远期支付”,另一种为“保证金中途返还”, 现在需求删除保证金返还方式,也就是说全部在期末返还,避免了这些特殊情况。
- 受资金计划影响,现金流中也有计入XIRR这一字段,否则无法进行XIRR的计算;
- 所有租金计划都是计入XIRR的,只有资金计划可以对该值进行修改;
存续TCR
存续TCR计算数据目前全部来源于“当年末累计收益”和“当年末累计资金占用”,所以计算过程中先要计算出以上两个值,其他的皆可推导。 注意点:如果遇到当期跨年的,则需要将当期拆开,分别计入上一年数据和下一年数据。
调息
调息是由于国家对存贷款利率进行调整,主要是为了控制物价、房价等。在央行发布调息利率以后,租赁公司可以选择根据央行基准利率进行调整,确定调息日进而将租金 在调息日以后的资金占用采用新的利率计算,进而影响租金。算法选择根据租金测算表中涉及调息字段决定,算法选择规则如下图所示:
